Published at 2022-09-17 14:52
Author:zhixy
View:2310
统计学上,自由度是指当用样本的统计量来估计总体的参数时,样本中独立的或能够自由变化的观测值个数,称为该统计量的自由度。
举例说明。假设我们要从一个总体中抽出10个观测值作为一组样本。因为抽样是随机进行的,而且抽样的过程可以重复多次,所以这10个观测值可视为10个独立的随机变量,它们的取值可自由变化。
注意:这里随机变量和统计学中定义——“相同性质的事物间表现差异性的某项特征或形状称为变量”,有所不同。
在用公式1计算样本的平均数时,只有10个观测值参与了计算。因此,对10个随机观测值的一组样本而言,计算平均数时的自由度为,即10个观测值都是可以自由变化的。
而当用公式2计算样本的方差时,10个观测值参与了计算,同时还有一个衍生量——即样本平均数。样本平均数在这里直接导致10个观测值,至少有一个不能自由变化。这时该组样本在计算样本方差时的自由度为。
这里我们可以说:“样本平均数限制了10个观测值中某一个观测值的自由变化”。为什么会这样呢?
样本平均数对自由度的影响与样本平均数的重要特性之一——“离均差之和为零”,有关。
样本平均数的重要特性二:“离均差平方和最小”。
在公式2中,因为总体平均数未知,只能用样本平均来代替 (估计)。公式2分子部分中的每一项离均差,受到“和为零”的限制。对10个观测值的样本来说,即
中有9个观测值可以自由变化,而最后一个观测值必须让10个离均差之和为零。这就是,“样本平均数限制了10个观测值中某一个观测值的自由变化”,的原因。
总的来说,计算不同的统计量,样本观测值的自由度是不同的,等于变量个数减掉其衍生量的个数。
那么,为什么在计算样本方差需要用自由度为分母呢?
统计学中,总体永远是我们研究的终极目标。
而由于总体的无限性或出于控制成本的目的,研究总体的手段是利用随机抽样获得样本,进而通过研究样本的性质,来估计总体的性质。
比如,用样本平均数来估计总体平均数,用样本方差来估计总体方差。
估计是统计推断中的两个主要内容之一。
常识上,我们都知道只要是估计,都可能有误差;当然估计也可能的非常准确。
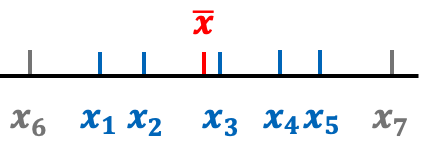
如上图所示,从一个总体中随机抽取了5个观测值:,它们有平均数
。这里的
表示没有被抽到的,同时又超出样本最小值 (
) 和最大值 (
) 覆盖范围的样本个体。
当我们用样本平均数来估计总体平均数时,之类的未抽到观测值对估计的效果不会有较大影响,因为样本覆盖范围左侧的值 (如
) 和右侧的值 (如
) ,即使抽到了也会在计算平均数的过程中相互抵消。
也就是说,即使是小量样本也可以得到对总体平均数较为准确的估计。
当然这里的前提是,抽样没有较大误差,也就是说总体平均数应该在样本覆盖的范围内。如果总体平均数大于或小于
,则抽样误差较大,那些样本覆盖范围之外的观测值的缺失就对估计产生严重影响了。
现在再来看用样本方差来估计总体方差的情况。
由于计算方差时,离均差是进行平方后再求和的,所以样本覆盖范围两侧的、未被抽到的观测值,它们的离均差平方不会像离均差那样相互抵消。
也就是说,未被抽到的观测值,它们偏离平均值的程度 (这也是方差所要衡量的),不会被考虑在内,即
其中样本容量为,
为总体中未被抽到的个体数量。所以,
注意:不等式右边样本平均数
,当抽完总体中的所有个体 (
个) 时,等于总体平均数
。
换句话说,像平均数的计算那样,用分母等于的方式计算出来的样本方差
永远小于总体方差。
为了让总体方差的估计更准确,方法就是将分母调小为
。
为什么把分母调小为自由度就可以了?调小为
可以吗?我们接着分析。
既然直接用样本容量作分母的样本方差来估计总体方差,总是偏低。那么,总体方差的“无偏的”估计该是怎么样的呢?
了解无偏估计之前,首先了解一下数学期望的概念。
假设有一随机变量,有有限个观测值
,且每个观测值的概率分别为
,则随机变量
的数学期望为
而如果该随机变量为连续性随机变量,则其数学期望为
其中为变量
的概率密度函数,有参数
个参数
。
本质上,数学期望就是对事件长期价值的数字化衡量。而方法上,数学期望就是对随机事件不同结果的概率加权平均。
由于每次抽样不同,样本的平均数也将表现为一个随机变量,那么样本平均数的期望,即样本平均数的平均数,有
可见样本平均数的数学期望等于总体平均数。换句话说,样本平均数是总体平均数的无偏估计。
同样的道理,我们可以对样本的方差 (仍然以样本容量作分母) 作如下推导:
注意以上推导过程,用到了公式
,且有使用了两次。
所以总体方差与样本方差的数学期望并不相等,而有
这就是样本方差应该用自由度作分母的本质原因。
自由度在统计学的相关概念中,属于让人头疼的那一类,而且出现的频率还比较高。如一时不能理解透彻,也应留心,日后慢慢消化。
数学上,我们知道要对总体方差作无偏估计,样本方差计算公式中的分母应该调为。实际上是样本的二阶中心矩
乘以一个大于1的系数
。
矩的概念由统计学家K. Pearson确立的,包括原点矩和中心距。在此不详述。
对总体方差的估计,实际上用二阶中心矩来估计的,但是每当用二阶中心矩来估计时都会偏低,所以需要乘以系数。
