Published at 2021-06-20 20:25
Author:zhixy
View:1457
系统发育树的可能数量随着分类群的数量呈超指数级增长。在许多情况下,这样的组合爆炸意味着优化问题,即找到最大似然 (maximum likelihood, ML) 树,在计算机科学中被称为NP难题 (NP-hard)。
NP是指非确定性多项式 (non-deterministic polynomial, NP)。所谓的非确定性是指,可用一定数量的运算去解决多项式时间内可解决的问题。
简单的说,NP难题意味着不存在任何已知的算法用一定数量的运算去解决多项式时间内可解决的问题。在我们的例子中,输入大小是分类单元的数量和输入位点的数量,即我们想要推断出树的相关分类单元的多序列比对 (multiple sequence alignment, MSA)。
利用理论计算机科学的机制,已经证实基于简约和ML等树评分标准寻找最优树的方法是非常困难的。换句话说,我们需要计算每一个可能树的似然分数才能找到ML树。
由于今天的计算机的强大能力,乍一看,这可能并没有问题。然而,假设我们想在一个有100个分类单元的MSA上推断一个ML树,根据目前的标准,这只是一个关于分类单元数量的中型数据集。然而对于这个数据集,大约有个不同的无根系统发育树。
据TreeCounter的计算,100个类群可能的无根二叉树的确切数量是:1700458809293409622837847870503541607357725018410424900227835868363625808886 28332485131901009696411611113290250954694628264213300391989811682923929339908 722247494604289531707763671875
简便起见,假设在一棵树上计算似然分数时需要1秒。要找到ML树,必须对所有个树进行评分。这需要的总体运行时间约为
年,这相当于于宇宙年龄的
倍。值得注意的是,使用强大的并行超级计算机并不能减少相对较长的等待时间,因为超算只是线性地减少运行时间,而不是超指数级的。假设我们可以使用一台拥有
个处理器的超级计算机,仍然需要等待
倍的宇宙时间。
大概谁都不想等待这么长时间,所以需要设计启发式搜索策略 (heuristic search strategies),以一种“智能”的方式穿越巨大的树空间,并返回一个有“好”分数的树。目前使用的大多数启发式方法都是临时的策略 (ad hoc strategies)。换句话说,它们并没有从任何理论上保证,找到的树离全局最优树有多近或多远。这也是为什么我们在经验进化生物学论文中,经常看到具有潜在误导性的术语的原因。论文通常是指“ML树”,然而这只是由完全临时的启发式搜索策略所发现的最好系统发育树。
人们可能会对贝叶斯推理的计算复杂度感兴趣,因为它本质上也依赖于对树的重复似然评估,也会假设它们的复杂度也一定是受巨大树空间影响。如果我们简单地看贝叶斯方程:
其中表示树,
表示MSA数据,
表示树的先验概率,
表示树
的标准系统发育似然评分。计算问题隐藏在
中,它表示数据不能精确计算的,但需要近似的边缘概率。对于ML法,对这一项的精确评估需要计算所有可能树拓扑结构的似然分数,在贝叶斯方法中,也需要计算所有可能的剩余参数值 (例如分枝长度、核苷酸替换率等)。因此,精确地计算
甚至需要比ML更长的等待时间。因此,人们放弃了精确地计算后验概率
。作为一种解决方法,后验概率用马尔可夫链蒙特卡罗 (Markov-Chain Monte-Carlo, MCMC) 方法进行近似。不幸的是,MCMC链只有在运行无穷大时间时,才保证收敛于真实的后验分布。在实践中,MCMC链收敛性的缺乏可以使用所谓的收敛性分析工具来评估,但这些方法不能用来证明链已收敛。基于MCMC的数学基础,如果永远运行下去,链才会而且只会收敛到真实的后验概率分布。因此,收敛性分析工具只能检测到缺乏收敛性。如果结果为不缺乏收敛,那么就表明MCMC过程已经达到了一个明显收敛的领域。
在以下部分中,我们将自上而下介绍ML树搜索算法。
首先,我们将讨论构成几乎所有基于ML的树状搜索算法的一部分基本组件。大多数搜索策略都包括以下两个步骤:
最广泛使用的基于ML的软件工具 (RAxML, IQ-Tree, PHYML和GARLI) 都实现了这一策略。然而,研究人员也尝试了分而治之法,综合树是通过混淆 (puzzling) 独立优化的子树而组合起来的。
构建一个综合的起始树至少有三种解决方案:选择随机树拓扑,建邻接树 (neighbor-joining, NJ) 或其变体 (如BioNJ),和建简约树。正如主要在贝叶斯系统发育推断中所做的那样,我们可以简单地构建一个完全随机起始树 (complete random starting tree)。或者可以选择使用一种更简单的树构建方法,推断出一些合理的树 (如NJ树)。NJ起始树通常比完全随机树有更好的似然分数。但仅使用NJ树,可能会驱使随后的树搜索陷于局部最优值。由于巨大的树空间可能会表现出很多局部最优,因此希望实现某种机制 (通常依赖于某种随机化),以允许搜索以某种方式跳出局部最优。这可以通过生成一组不同的起始树,或通过树搜索过程中的随机化步骤来实现。目前,我们将专注于生成不同的起始树。如果我们的软件工具采用了完全随机起始树,获得一组个不同的起始树是简单直接的,因为我们只需要随机生成
个综合树。
如果我们想获得一组不同的起始树,且具有比随机树更好的初始似然分数,我们可以使用所谓随机逐步添加算法 (randomized stepwise addition algorithm),并采取简单的标准来评价这些新生成的树。这里意味着,相对于似然计算,时间成本较低的标准。简约或最小二乘标准是这种简单标准的好例子。这些合理而简单的标准将产生具有“良好”初始似然评分的起始树。因此,随后在综合树上的搜索可能收敛得更快,从而减少了推断时间。具体示例详见下图。
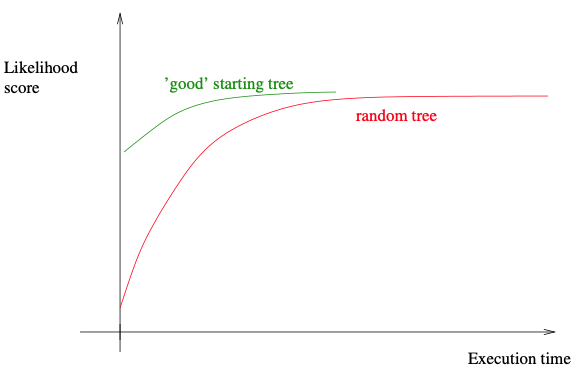
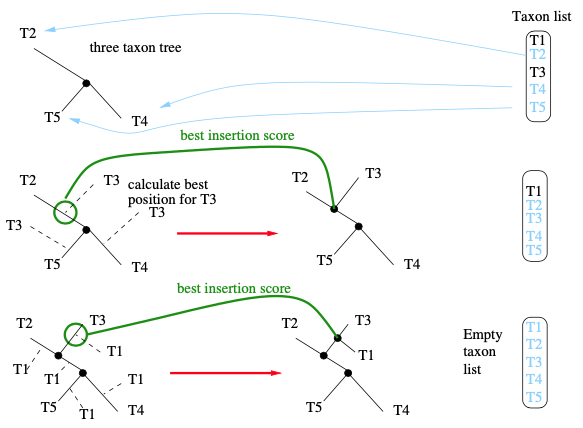
下面,我们将简要概述给定一个具有个类群的MSA的随机逐步添加算法。
一般来说,多次使用不同的随机分类单元添加顺序 (例如按t1、t2、t3、t4、t5这个顺序插入和按t3、t1、t5、t5、t2、t4顺序插入),我们将获得一组拓扑上不同的综合初始树。然而,如果数据中的系统发育信号非常强,几个不同的添加顺序会产生相同的树。因此,我们应该首先在对这些树启动计算密集型ML搜索之前,通过计算所有起始树之间的Robinson-Foulds距离 (RAxML-NG软件的-rfdist命令可实现),来检验的起始树集包含了多少不同的树。
由于ML的计算成本,我们通常不使用似然作为这个随机逐步添加程序的标准。在所有基于似然的树推断工具中,评估树上的可能性需要整个运行时的85%-95% (这也适用于贝叶斯推理)。此外,在这一步中使用似然并不会产生比使用简约评分更好的树。此外,人们通常会通过对综合树应用拓扑变化来观察到更大的改进可能性。因此,使用简约或NJ/BioNJ,代表了初始树的质量 (似然分数) 和构建它所需的时间之间工程学权衡。值得一提的是,一些较旧的工具,即fastDNAml和PAUP*,使用最大似然作为选项实现了随机逐步添加程序。
最后,使用基于简约评分的随机逐步添加起始树 (如RAxML或IQ-Tree),可能会偏向于搜索树空间的特定部分和特定的局部最优。因此,依赖于综合起始树和随后贪婪搜索策略可以受益于使用起始树类型 (如随机树和简约树) 来更彻底地探索树空间。一般来说,这需要根据手上的数据,根据具体情况进行评估。我们想象搜索空间的方式如下图所示。
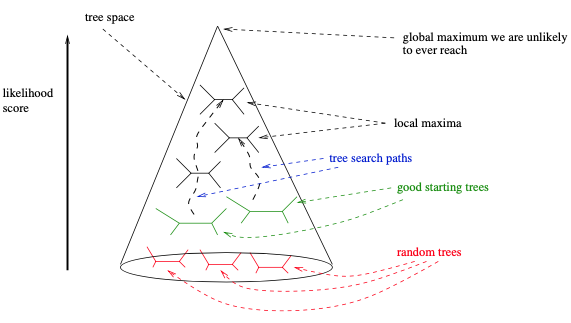
如前所述,大多数贝叶斯推断程序通常从一个随机树开始。不过一些软件,如MrBayes和ExaBayes,也选择在随机逐步添加顺序简约树上启动MCMC过程。
现在我们知道了如何计算一个综合起始树,现在可以考虑改变该树的基本技术,以进一步提高似然分数。
我们首先只考虑广泛使用的标准树变动 (tree moves) 方法 (允许我们不同程度地改变树的分枝关系)。换句话说,我们将考虑较大程度的改变树拓扑 (粗线条的变动),和轻微改变树拓扑 (细线条的变动)。在讨论树变动时,我们总是将给定的树称为当前树 (current tree)。它可以是到目前为止找到的最好的树,并存储在内存中。通过树变动,我们尝试通过改变当前的树来构建一个新的树,希望这棵新树能比当前的树有更好的似然分数。
广泛使用的基本树变动 (也称为拓扑改变机制) 方法有以下三个:
最简单和最保守的树变动方法是NNI。要应用NNI,我们首先需要选择树的一个内部分枝 (搜索策略需要考虑的内容)。在图4的示例中,蓝色子树和红色子树位于该内部分枝的一边,黄色的和绿色的在另一边。为了使用NNI生成一个新的树,现在可以在内部分枝上翻转彩色子树。因此,从包含这个内部分枝的树,我们可以构建两个新的,但没有实质性不同的树拓扑,并估计它们的似然分数。
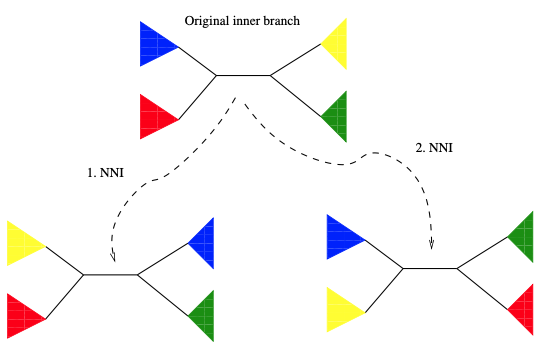
相对于“细线条的”NNI,SPR则算是“粗选条的”。执行SPR变动,我们首先在综合树中选择子树的根。同样地,选择这样一个根的顺序取决于实际的树搜索策略。在RAxML中,我们首先进行深度优先的树遍历,并将SPR变动应用到我们遇到的所有子树。一旦我们选择了一个子树 (称为候选子树 candidate subtree) 的根,首先通过从包含该子树根的分枝中剪掉子树。从当前树中剪掉子树的原始分枝,被称为剪切分枝 (pruning branch)。然后开始插入,并计算似然分数,并再次删除候选子树,并移动到剪枝分枝的邻近分枝上。我们可以通过所谓的重排半径 (rearrangement radius) 来定义该邻居的大小 (见图5)。重排半径允许我们确定离剪枝分枝有多少节点,我们想要重新插入候选子树的范围。如果重排半径设置为1,将只执行保守的SPR变动 (距剪切分枝只有一个内节点);而如果我们将重排半径设置为树中内部节点的总数 (个分类群的无根二叉树内部节点总数为
),我们执行“粗线条的”变动并探索更大的树空间。如何设置这个重排半径?如何将其适应手上的MSA?以及如何在树搜索过程中潜在地改变它?都是搜索策略方法开发所要考虑。在RAxML中,默认是使用以下策略自动确定“良好”重排半径:选择对起始树产生似然分数改进最大的、最小SPR半径。在大多数其他工具中,重排半径设置为固定的默认值,但用户可以通过各自的命令行参数进行更改。
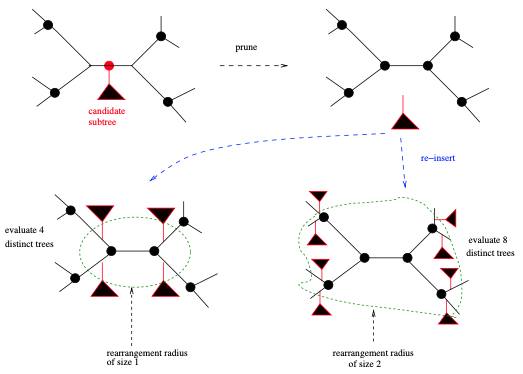
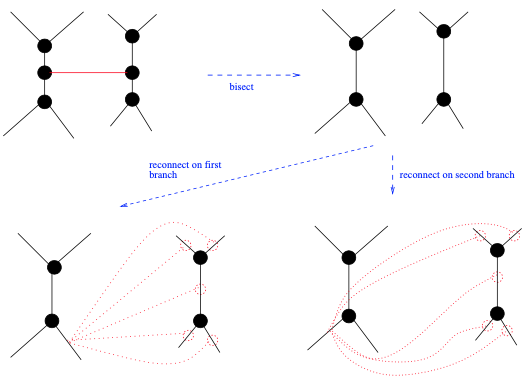
最“粗线条的”变动是TBR (见图6),因为它可以在树上引起巨大的拓扑变化。也因此,TBR可以大幅增加或减少生成树的似然分数。为了执行TBR,人们首先选择一个分枝来将当前树一分为二,以获得两个未连接的子树和
。然后,通过重新连接这两个子树来生成替代树拓扑。重新连接的方式,由两个子树的分枝决定。我们可得到
个替代树拓扑,其中
是
中的分枝数,
是
中的分枝数。与SPR类似,我们可以将这些重新连接操作的范围限制在原始截断分枝的附近。
这三个基本的树变动似乎是相对直接的。为了最大化计算效率,也就是说,最小化系统发育似然分数的计算,在实践中应用了大量的快捷和启发式方法。原则上,在每个树变动之后,例如,在应用NNI之后,需要重新优化所有分枝长度和所有其它的模型参数 (包括GTR速率,伽马分布的形状参数,模型速率异质性等),以获得新生成树的最大似然分数。由于系统发育的全局优化操作是高度计算密集型的,因为它们需要反复遍历和重新计算整个树的似然分数,所有常见的基于ML的树推断程序都使用快捷方式。换句话说,他们只计算通过树变动生成树的近似似然分数。
ML软件开发人员通常使用以下三种快捷方式。
为了规避除分枝长度以外的重新估计ML模型的参数 (GTR速率,形状参数) 的高计算成本,依赖于以下经验观察:只要应用的树是合理的 (即非随机的),模型参数估计就不会发生重大变化。因此,只有在对树拓扑应用了相对大量的树变动和潜在拓扑变化之后,才会周期性地重新估计它们。
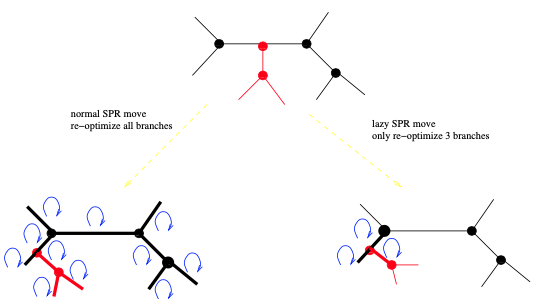
为了避免在变动后重新估计新树的所有分枝长度,我们认为:分枝长度受变动影响最大的应该是,发生更改的所在区域,因此只有那些据说是受影响最大的分枝长度才会被重新估计。例如,考虑一个NNI变动。这里假设图4中黑色显示的5个分枝是NNI变动影响最大的。因此,只需在应用NNI后重新估计这5个分枝的长度。人们甚至可以决定只重新估计中心的分枝。最有效的是在程序开发过程中,在基准数据集上进行的许多试错实验。对于SPR变动,可以应用RAxML中引入的所谓惰性SPR变动技术。此处,仅重新估计靠近子树插入位置的三个分枝长度 (见图7)。在GARLI中,有一种更详细的方法来进行惰性SPR变动。GARLI试图动态地确定变动后需要重新估计的分枝数量。换句话说,它在距离子树插入位置的递增距离上优化分枝长度,直到它们不再发生显著变化。
为了避免在应用拓扑变动时,在树的遥远区域之间来回跳跃,大多数ML搜索算法以预定义的顺序系统地将变动应用到树上 (例如深度优先树遍历)。这提高了计算的效率,因为变动总是只发生在树的一个区域,而树的其余部分没有变化。然后,变动到邻近区域 (例如邻近的子树,试图随着SPR变动重新排列)。
有了基本的树变动方法,现在可以设计树搜索策略。大多数流行的搜索算法会将其中一个或多个变动重复应用到当前树上,直到没有变动会产生ML分数更好的树。一旦不能应用任何可以进一步提高ML分数的变动,该算法就会收敛并返回它能够找到的得分最好的ML树。
在原始版本的PHYML中实现的一种简单的搜索策略:
如此简单的搜索策略的关键缺陷是,它很可能在早期被困在如下图所示的局部最优区域内。缓解这种情况的一种方法是使用“组线条的”变动,如SPR或TBR。它们允许相对容易地离开这样的局部最优值。RAxML和GARLI主要依赖于惰性SPR,而PHYML版本3也引入了SPR移动。此外,还可以对几种不同的随机添加顺序简约起始树进行多个树搜索 (例如RAxML和IQ-Tree)。虽然这些搜索策略在收敛时仍然很可能陷入局部最优,但这些局部最优值会比上述简单算法会陷入的局部优值高。
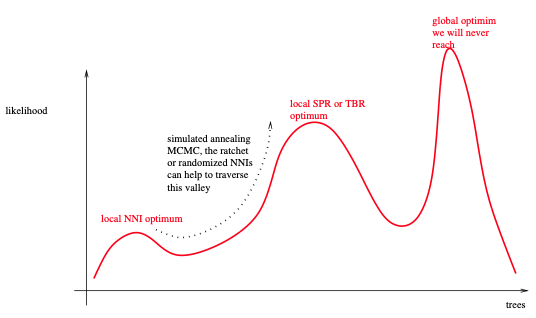
由于IQ-Tree主要依赖于NNI变动,因此更容易陷入局部最优区域,除了使用不同的简约起始树,它采用了一种附加技术。一旦它被困在所谓的NNI最优值中,它就会应用一些完全随机的NNI变动 (而不考虑这些变动生成树的似然分数)。这种操作会充分地扰动树,并离开本地最优状态。在这种扰动之后,应用了新一轮的NNI来提高ML分数,这很可能以一个不同的、但更好的局部最优结束。
通过随机扰动跳出局部最优的另一种方法是棘轮法 (ratchet method)。这个想法是:首先随机更改MSA位点的权重,然后将一些NNI或SPR应用到这个扰动过的MSA,然后恢复原始的MSA。然后,我们将搜索策略重新应用到扰动过的MSA生成的新树上。GARLI 使用了一种所谓的遗传算法来逃避局部最优值。GARLI不是在一棵树上进行搜索,而是对一群树进行搜索。在群内的不同树之间定期交换信息,以提高整个树群的质量。
局部最优逃逸的另一个选择是使用模拟退火搜索技术 (simulated annealing search)。模拟退火允许执行后退步骤,也就是说,它偶尔会将搜索移动到ML分数较低的树。这可能允许在简约法和ML树搜索中走出局部最优值。值得注意的是,模拟退火与贝叶斯MCMC采样非常相似,因为MCMC链偶尔也会接受所谓的下坡步骤 (downhill steps) 来对具有较低后验概率的树进行采样。
最后,还存在着所谓的“粗糙的似然表面 (rough likelihood surface)”的问题。当分析具有相对较少的位点和大量的分类群的数据集时 (例如包含100或更多个分类群的16S rRNA基因),通常会出现这样一个粗糙的似然表面。也就是说搜索空间将出现大量的局部最优,(i) 不能使用标准的基于似然的显著性测试 (CONSEL) 相互区分;(ii) 显示平均超过20%甚至30%的较大的成对拓扑距离。Stamatakis (2011) 使用一个经验的单基因数据集给出了一个较为粗糙的似然表面的例子。一般来说,这类数据集的关键挑战是100次不同的ML搜索可能产生100个拓扑结构上非常不同的,但统计上又无法区分的树。
粗糙的似然表面,对应于系统发育分辨率不足的问题。
到目前为止,我们已经简要地讨论了最流行的ML树搜索策略是如何工作的。设计系统发育搜索策略的另一种方法是应用分而治之策略 (divide-and-conquer strategy)。其想法是:开始时将输入序列分割为不相交的或部分重叠的密切相关的序列集 (例如简单地通过聚类序列或使用简约树),然后在这些子集上推断单个树,最后将这些子树合并成一个大的综合树。只要序列子集重叠,该合并步骤也可解释为一个超树 (supertree) 重建问题。
一般来说,所有为ML设计的分治树搜索算法的尝试,在速度和精度的改进方面并没有特别成功。结果证明,到目前为止设计的所有分治方法都需要对树的拓扑、分枝长度和模型参数进行额外的全局优化。对在综合树上进行额外全局优化的要求也对分治法可能产生的潜在速度节约产生了负面影响。
虽然这一点还没有被正确地理解,但我们怀疑对综合树进行全局优化是必须的,因为从单个子树传播的关于分枝长度和模型参数的信息,对其余子树的树拓扑和分枝长度有重要影响。换句话说,我们试图解决的子问题 (子树) 似乎不是相互独立的,以允许应用分而治之的方法。一个有点相关的方法是在Tree-Puzzle中实现的四重混淆 (quartet puzzling) 想法。它最初从MSA建造四重树 (quartet tree,有4个分类群的树),然后把它们一起拼图成一棵完整的树。
最近发现的一种影响基于似然的系统发育推断 (ML和BI) 的现象是,树空间中的梯台 (terrace)。terrace是一个潜在的大集合,包含拓扑结构不同的树,但具有完全相同的解析似然分数。由于舍入误差传递 (round-off error propagation),数值似然值可能略有增加。
理论上的树空间,经过似然计算,可以映射到一条似然分数曲线。在这条曲线上应该存在一个极大值点,对应于最优的系统发育树。terrace指的是这条曲线上出现的梯田式的平台,在这个“梯台”上似然分数是相等或非常相近的。但与这些似然分数所对应的树却有显著的拓扑结构差异。
在似然框架下,当使用非关联 (unlinked) 的分枝长度估计时,terrace可能会出现在分区的系统发育基因组多序列比对中。当我们为每个系统发育基因组多序列比对的分区(partition) 获得一个完全独立的分枝长度估计集合 (一个分区一个集合) 时,分枝就是非关联的。只有在分枝长度非关联时,才会出现terrace,因为串联MSA (supermatrix) 的整体似然分数是独立优化的每个分区似然分数的总和。与此相反,当分枝长度是关联的 (即联合分支长度估计),不能单独对每个分区进行独立的优化。换句话说,分区通过共享的分枝长度值以某种方式相互连接,就防止了terrace的出现。
在分区的系统发育基因组多序列比对数据中,通常一个基因为一个分区 (partition)。
如果MSA(在非关联的分枝模型下)和各自的分区方案包含一个或多个terrace,取决于缺失数据的模式。因此,在设计树搜索方案时,应该避免能够将搜索带到同一terrace上另一个树的变动,或者至少省略这种冗余的计算。在2011年被数学描述之前,在RAxML原型中实现的省略不必要的似然计算的树变动,是由 Stamatakis 和 Alachiotis (2010) 开创的,基本上是通过对terrace的隐式识别。后来,Chernomor利用更优雅的数据结构,提出了省略标准树变动操作中冗余计算的工作,通过IQ-Tree进行了实现。
虽然在RAxML和IQ-Tree中实现的技术允许避免在terrace上的冗余似然计算,但它们不提供在树空间中离开terrace的明确机制。terrace不仅与降低ML搜索的计算成本有关。它们也会误导下游的分析。例如,terrace的存在可能会导致严重的自展值和贝叶斯支持值的偏差。目前还不清楚有多少已发表的系统发育树确实是从terrace上获取的。Dobrin等 (2018) 分析了26个大型经验系统发育数据集,表明terrace存在于几乎所有数据集中,而在自展重采样过程中发现的terrace降低了整体支持度。其中一个原因是,标准的系统发育推断工具不会常规地评估它们生成的最后一棵树是否来自于terrace。然而,现在已经开发了一个C库用于识别terrace,并集成在RAxML-NG中。
在进行经验系统发育研究时,对树上分枝支持度的推断是一个重要内容。标准方法是由 Felsenstein (1985) 提出的非参数自展 (bootstrap, BS)。BS的思想是从原始MSA中随机地、有替换地进行采样,以生成一套100个或更多稍微不同的MSA自展复本。然后,将在原始MSA上推断进化树的相同算法应用于每个自展复本。这将生成一组100个 (或更多) BS树,这些树随后可用于构建一致树 (consensus tree),或将分枝支持度映射到在原始MSA上推断出的最优ML树。Lemoine等最近提出了一种更详细的方法,将BS支持度映射到给定树,同时考虑到各自树空间的大小。
支持度由相同分枝在所有BS树中出现的频率表示,通常以百分数的形式。
很难确定需要多少BS复本,但它似乎在很大程度上依赖于手上的数据。
显然,自展分析在计算上是非常昂贵的。已有一些尝试试图加快自展分析,而采用近似的方法来推断系统发育的支持度。值得注意的是,它们代表着“近似的近似”,因为找到最优ML树是NP困难的,目前的树搜索策略已经代表了临时的启发式方法。因此使用这些快速的方法来推断支持值,总是被批评为过于近似。
这里建议:“如果数据集的大小和可用的计算资源允许,那么最好使用具有标准自展程序的标准搜索策略来进行BS复本搜索。”
在RAxML中,引入了所谓的快速自展程序,它基本上依赖于标准RAxML搜索算法的一个更近似、更不彻底的版本,它更容易被困在局部最优值中。在IQ-Tree中实现的所谓超快自展依赖于在原始MSA搜索过程中,对模拟BS复本的进行近似采样。因此,这在很大程度上取决于在原始MSA上的搜索所探索的树空间区域,是否也构成了BS复本树搜索空间的一部分。换句话说,需要树搜索空间的两个区域 (原始MSA区域和BS复本MSA区域) 经常重叠,以便近似更精确。然而,这并不是能得到预先保证的。
最后,近似似然比检验 (approximate likelihood ratio test, aLRT) 采用给定的最优ML树,并通过计算该分枝周围的三种可能NNI变动的似然分数,将它们作为检验统计量,对树的每个内部分枝进行统计检验。aLRT计算检验统计量,因完全依赖基于NNI的似然,而受到批评。
上述所有获得支持度的近似值都是有用的。尽管如此,它们仍然是一个近似值,所以容易受到批评。
这里我们介绍了最大似然框架下,常用树搜索策略的基本组件,树变动操作,和树搜索策略。此外,我们还讨论了推断树上支持度的标准系统发育自展程序,以及该任务的一些更快、更近似的方法。还简要地回顾了寻找ML树的时间复杂度,并解释了NP困难概念背后的意义。最后,我们还简要地概述了当要分析的数据集在其树搜索空间中包含所谓的平台时所出现的其他问题。
我们应该记住,所有的树搜索工具都实现了临时的启发式搜索策略,这些策略是基于一些模拟和一些经验基准测试数据集开发和测试。因此面对实际数据,它们有可能还是会失败,也就是说,在不同或麻烦的设置下,在其他数据集上搜索策略呈现次优表现。此外,这里提出的搜索策略没有任何性能保证,即它们推断的树离全局最优树有多远是未知的。
最好的方法是使用几种ML树推断工具来进行搜索,还可以结合贝叶斯系统发育推理的工具,并比较它们的结果。这也有助于尽量减少潜在编程错误的影响,因为树推断工具软件已经变得更复杂,支持比10-15年前更复杂的模型。
全文翻译自:Alexandros Stamatakis and Alexey M. Kozlov (2020). Ecient Maximum Likeli- hood Tree Building Methods. In Scornavacca, C., Delsuc, F., and Galtier, N., editors, Phylogen- etics in the Genomic Era, chapter No. 1.2, pp. 1.2:1–1.2:18.
